Таблица производных обратных тригонометрических функций. Производные простых тригонометрических функций

Представлены производные обратных тригонометрических функций и вывод их формул. Также даны выражения производных высших порядков. Ссылки на страницы с более подробным изложением вывода формул.

Сначала выведем формулу производной арксинуса. Пусть
y = arcsin x .
Поскольку арксинус есть функция, обратная к синусу, то
.
Здесь y - функция от x . Дифференцируем по переменной x :
.
Применяем :
.
Итак, мы нашли:
.

Поскольку , то . Тогда
.
И предыдущая формула принимает вид:
. Отсюда
.

Точно таким способом можно получить формулу производной арккосинуса. Однако проще воспользоваться формулой, связывающей обратные тригонометрические функции :
.
Тогда
.

Более подробно изложение представлено на странице “Вывод производных арксинуса и арккосинуса ”. Там дается вывод производных двумя способами - рассмотренным выше и по формуле производной обратной функции.

Вывод производных арктангенса и арккотангенса

Таким же способом найдем производные арктангенса и арккотангенса.

Пусть
y = arctg x .
Арктангенс есть функция, обратная к тангенсу:
.
Дифференцируем по переменной x :
.
Применяем формулу производной сложной функции :
.
Итак, мы нашли:
.

Производная арккотангенса:
.

Производные арксинуса

Пусть
.
Производную первого порядка от арксинуса мы уже нашли:
.
Дифференцируя, находим производную второго порядка:
;
.
Ее также можно записать в следующем виде:
.
Отсюда получаем дифференциальное уравнение, которому удовлетворяют производные арксинуса первого и второго порядков:
.

Дифференцируя это уравнение, можно найти производные высших порядков.

Производная арксинуса n-го порядка

Производная арксинуса n-го порядка имеет следующий вид:
,
где - многочлен степени . Он определяется по формулам:
;
.
Здесь .

Многочлен удовлетворяет дифференциальному уравнению:
.

Производная арккосинуса n-го порядка

Производные для арккосинуса получаются из производных для арксинуса с помощью тригонометрической формулы:
.
Поэтому производные этих функций отличаются только знаком:
.

Производные арктангенса

Пусть . Мы нашли производную арккотангенса первого порядка:
.

Разложим дробь на простейшие:

.
Здесь - мнимая единица, .

Дифференцируем раз и приводим дробь к общему знаменателю:

.

Подставляя , получим:
.

Производная арктангенса n-го порядка

Таким образом, производную арктангенса n-го порядка можно представить несколькими способами:
;
.

Производные арккотангенса

Пусть теперь . Применим формулу, связывающей обратные тригонометрические функции:
.
Тогда производная n-го порядка от арккотангенса отличаются только знаком от производной арктангенса:
.

Подставив , найдем:
.

Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.

Для нахождения производной тригонометрической функции нужно пользоваться таблицей производных , а именно производными 6-13.

При нахождении производных простых тригонометрических функций во избежание распространённых ошибок следует обращать внимание на следующие моменты:

• в выражении функции часто одно из слагаемых представляет собой синус, косинус или другую тригонометрическую функцию не от аргумента функции, а от числа (константы), поэтому производная этого слагаемого равна нулю;
• почти всегда нужно упростить выражение, полученное в результате дифференцирования, а для этого нужно уверенно пользоваться знаниями по действиям с дробями;
• для упрощения выражения почти всегда нужно знать тригонометрические тождества, например, формулу двойного угла и формулу единицы как сумму квадратов синуса и косинуса .

Пример 1. Найти производную функции

Решение. Допустим, с производной косинуса всё понятно, скажут многие, начинающие изучать производные. А как быть с производной синуса двенадцати, делённых на пи? Ответ: считать равной нулю! Здесь синус (функция всё-таки!) - ловушка, потому что аргумент - не переменная икс или любая другая переменная, а просто число. То есть, синус этого числа - тоже число. А производная числа (константы), как мы знаем из таблицы производных, равна нулю. Итак, оставляем только минус синус икса и находим его производную, не забывая про знак:

.

Пример 2. Найти производную функции

.

Решение. Второе слагаемое - тот же случай, что и первое слагаемое в предыдущем примере. То есть, число, а производная числа равна нулю. Находим производную второго слагаемого как производную частного:

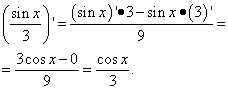
Пример 3. Найти производную функции

Решение. Это уже другая задача: здесь в первом слагаемом нет ни арксинуса, ни другой тригонометической функции, но есть икс, а значит, это функция от икса. Следовательно, дифференцируем её как слагаемое в сумме функций:

Здесь потребовались навыки в действиях с дробями , а именно - в ликвидации трёхэтажности дроби.

Пример 4. Найти производную функции

.

Решение. Здесь буква "фи" играет ту же роль, что "икс" в предыдущих случаях (и в большинстве других, но не во всех) - независимой переменной. Поэтому, когда будем искать производную произведения функций, не будем спешить объявлять равной нулю производную корня от "фи". Итак:

Но на этом решение не заканчивается. Так как в двух скобках собраны подобные члены, от нас ещё требуется преобразовать (упростить) выражение. Поэтому умножаем скобки на вынесенные за них множители, а далее приводим слагаемые к общему знаменателю и выполняем другие элементарные преобразования:

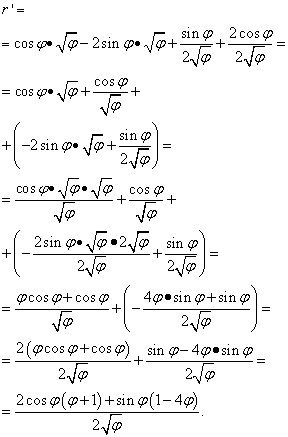
Пример 5. Найти производную функции

Решение. В этом примере от нас потребуется знание того факта, что существует такая тригонометрическая функция - секанс - и её формулы через косинус. Дифференцируем:

Пример 6. Найти производную функции

.

Решение. В этом примере от нас потребуется помнить из школьного курса формулу двойного угла. Но сначала дифференцируем:

,

(это и есть формула двойного угла)

Из курса геометрии и математики школьники привыкли, что понятие производной доносится до них через площадь фигуры, дифференциалы, пределы функций, а также лимиты. Попробуем посмотреть на понятие производной под другим углом, и определить, как можно увязать производную и тригонометрические функции.

Итак, рассмотрим некую произвольную кривую, которая описывается абстрактной функцией y = f(x).

Представим что график — это карта туристического маршрута. Приращение ∆x (дельта икс) на рисунке — это определенный промежуток пути, а ∆y – это изменение высоты тропы над уровнем моря.
Тогда получается, что отношение ∆x/∆y будет характеризовать сложно маршрута на каждом отрезке пути. Узнав это значение можно с уверенностью сказать крутой ли подъем/спуск, понадобится ли альпинистское снаряжение и нужна ли туристам определенная физическая подготовка. Но показатель этот будет справедлив только для одного маленького промежутка ∆x.

Если организатор похода возьмет значения для начальной и конечной точек тропы, то есть ∆x – будет равен длине маршрута, то не сможет получить объективные данные о степени сложности путешествия. Следовательно, необходимо построить еще один график, который будет характеризовать скорость и «качество» изменений пути, другими словами определять отношение ∆x/∆y для каждого «метра» маршрута.

Этот график и будет являться наглядной производной для конкретной тропы и объективно опишет ее изменения на каждом интересующем интервале. Убедиться в этом очень просто, значение ∆x/∆y – есть не что иное, как дифференциал, взятый для конкретного значения x и y. Применим же дифференцирование не определенным координатам, а к функции в целом:

Производная и тригонометрические функции

Тригонометрические функции неразрывно связаны с производной. Понять это можно из следующего чертежа. На рисунке координатной оси изображена функция Y = f (x) – синяя кривая.

K (x0; f (x0)) – произвольная точка, x0 + ∆x – приращение по оси OX, а f (x0 + ∆x) – приращение по оси OY в некой точке L.

Проведем прямую через точки K и L и построим прямоугольный треугольник KLN. Если мысленно перемещать отрезок LN по графику Y = f (x), то точки L и N будут стремиться к значениям K (x0; f (x0)). Назовем эту точку условным началом графика — лимитом, если же функция бесконечна, хотя бы на одном из промежутков – это стремление также будет бесконечным, а его предельное значение близким к 0.

Характер данного стремления можно описать касательной к выбранной точке y = kx + b или графиком производной первоначальной функции dy – зеленая прямая.

Но где же здесь тригонометрия?! Все очень просто рассмотрим прямоугольный треугольник KLN. Значение дифференциала для конкретной точки K есть тангенс угла α или ∠K:

Таким образом можно описать геометрический смымсл производной и ее взаимосвязь с тригонометрическими функциями.

Формулы производных для тригонометрических функций

Преобразования синуса, косинуса, тангенса и котангенса при определении производной необходимо заучить наизусть.

Последние две формулы не являются ошибкой, дело в том, что существует разница между определением производной простого аргумента и функции в том же качестве.

Рассмотрим сравнительную таблицу с формулами производных от синису, косинуса, тангенса и котангенса:

Также выведены формулы для производных арксинуса, арккосинуса, арктангенса и арккотангенса, хотя они применяются крайне редко:

Стоит отметить, что приведенных формул явно недостаточно для успешного решения типовых заданий ЕГЭ, что будет продемонстрированно при решении конкретного примера поиска производной тригонометрического выражения.

Задание : Необходимо найти производную функции и найти ее значение для π/4:

Решение : Чтобы найти y’ необходимо вспомнить основные формулы преобразования исходной функции в производную, а именно.

Тема: «Производная тригонометрических функций».
Тип урока – урок закрепления знаний.
Форма урока – интегрированный урок.
Место урока в системе уроков по данному разделу – обобщающий урок.
Цели поставлены комплексно:

• обучающие: знать правила дифференцирования, уметь применять правила вычисления производных при решении уравнений и неравенств; совершенствовать предметные, в том числе вычислительные, умения и навыки; навыки работы с компьютером;
• развивающие: развитие интеллектуально-логических умений и познавательных интересов;
• воспитательные: воспитывать адаптивность к современным условиям обучения.

Методы:

• репродуктивные и продуктивные;
• практические и словесные;
• самостоятельные работы;
• программированное обучение, Т.С.О.;
• сочетание фронтальной, групповой и индивидуальной работы;
• дифференцированного обучения;
• индуктивно-дедуктивный.

Формы контроля:

• устный опрос,
• программированный контроль,
• самостоятельная работа,
• индивидуальные задания на компьютере,
• взаимопроверка с применением диагностической карты учащегося.

ХОД УРОКА

I. Организационный момент

II. Актуализация опорных знаний

а) Сообщение целей и задач:

• знать правила дифференцирования, уметь применять правила вычисления производных при решении задач, уравнений и неравенств;
• совершенствовать предметные, в том числе вычислительные, умения и навыки; навыки работы с компьютером;
• развивать интеллектуально-логические умения и познавательные интересы;
• воспитывать адаптивность к современным условиям обучения.

б) Повторение учебного материала

Правила вычисления производных (повторение формул по компьютеру со звуковым сопровождением). док.7.

1. Чему равна производная синуса?
2. Чему равна производная косинуса?
3. Чему равна производная тангенса?
4. Чему равна производная котангенса?

III. Устная работа

Найти производную.
Вариант 1.		Вариант 2.
у = 2х + 5.		у = 2х – 5.
у = 4cos х .		у = 3sin х .
у = tg х + ctg х .		у = tg х – ctg х .
у = sin 3х .		у = cos 4х .
Варианты ответов.
	– 4sin х		– 3cos х
1/cos 2 х + 1/sin 2 х	1/cos 2 х –1/sin 2 х	1/sin 2 х –1/cos 2 х
	– 4sin4х		– 3cos3х

Обменяйтесь тетрадями. Отметьте в диагностических картах верно выполненные задания знаком +, а неверно выполненные задания знаком –.

IV. Решение уравнений с помощью производной

– Как найти точки, в которых производная равна нулю?

Чтобы найти точки, в которых производная данной функции равна нулю, нужно:

– определить характер функции,
– найти область определения функции,
– найти производную данной функции,
– решить уравнение f "(x ) = 0,
– выбрать верный ответ.

Задача 1.

Дано: у = х – sin x .
Найти: точки, в которых производная равна нулю.
Решение. Функция определена и дифференцируема на множестве всех действительных чисел, так как на множестве всех действительных чисел определены и дифференцируемы функции g (x ) = x и t (x ) = – sin x .
Используя правила дифференцирования, получим f "(x ) = (x – sin x )" = (x )" – ( sin x )" = 1 – cos x .
Если f "(x ) = 0, то 1 – cos x = 0.
cos x = 1/; избавимся от иррациональности в знаменателе, получим cos x = /2.
По формуле t = ± arccos a + 2n, n Z, получим: х = ± arccos /2 + 2n, n Z.
Ответ: х = ± /4 + 2n, n Z.

V. Решение уравнений по алгоритму

Найти, в каких точках обращается в нуль производная.

f (x ) = sin x + cos x

f (x ) = sin 2x – x

f (x ) = 2x + cos(4x – )

Ученик может выбрать любой из трёх примеров. Первый пример оценивается оценкой «3 », второй – «4 », третий – «5 ». Решение в тетрадях с последующей взаимопроверкой. Один ученик решает у доски. Если решение оказывается неверным, то нужно ученику вернуться к алгоритму и попытаться решить снова.

Программированный контроль.

Вариант 1		Вариант 2
y = 2х 3		y = 3х 2
y = 1/4 х 4 + 2х 2 – 7		y = 1/2 х 4 + 4х + 5
y = х 3 + 4х 2 – 3х . Решить уравнение y " = 0		y = 2х 3 – 9х 2 + 12х + 7. Решить уравнение y " = 0.
y = sin 2х – cos 3х .		y = cos 2х – sin 3х .
y = tg х – ctg(х + /4).		y = ctg х + tg(х – /4).
y = sin 2 х .		y = cos 2 х .
Варианты ответов.
При выводе самой первой формулы таблицы будем исходить из определения производнойфункции в точке. Возьмем , где x – любое действительное число, то есть, x – любое число из области определения функции . Запишем предел отношения приращения функции к приращению аргумента при : Следует заметить, что под знаком предела получается выражение , которое не являетсянеопределенностью ноль делить на ноль, так как в числителе находится не бесконечно малая величина, а именно ноль. Другими словами, приращение постоянной функции всегда равно нулю. Таким образом, производная постоянной функции равна нулю на всей области определения . Производная степенной функции. Формула производной степенной функции имеет вид , где показатель степени p – любое действительное число. Докажем сначала формулу для натурального показателя степени, то есть, для p = 1, 2, 3, … Будем пользоваться определением производной. Запишем предел отношения приращения степенной функции к приращению аргумента: Для упрощения выражения в числителе обратимся к формуле бинома Ньютона: Следовательно, Этим доказана формула производной степенной функции для натурального показателя. Производная показательной функции. Вывод формулы производной приведем на основе определения: Пришли к неопределенности. Для ее раскрытия введем новую переменную , причем при . Тогда . В последнем переходе мы использовали формулу перехода к новому основанию логарифма. Выполним подстановку в исходный предел: Если вспомнить второй замечательный предел, то придем к формуле производной показательной функции: Производная логарифмической функции. Докажем формулу производной логарифмической функции для всех x из области определения и всех допустимых значениях основания a логарифма. По определению производной имеем: Как Вы заметили, при доказательстве преобразования проводились с использованием свойств логарифма. Равенство справедливо в силу второго замечательного предела. Производные тригонометрических функций. Для вывода формул производных тригонометрических функций нам придется вспомнить некоторые формулы тригонометрии, а также первый замечательный предел. По определению производной для функции синуса имеем . Воспользуемся формулой разности синусов: Осталось обратиться к первому замечательному пределу: Таким образом, производная функции sin x есть cos x . Абсолютно аналогично доказывается формула производной косинуса. Следовательно, производная функции cos x есть –sin x . Вывод формул таблицы производных для тангенса и котангенса проведем с использованием доказанных правил дифференцирования (производная дроби). Производные гиперболических функций. Правила дифференцирования и формула производной показательной функции из таблицы производных позволяют вывести формулы производных гиперболического синуса, косинуса, тангенса и котангенса. Производная обратной функции. Чтобы при изложении не было путаницы, давайте обозначать в нижнем индексе аргумент функции, по которому выполняется дифференцирование, то есть, - это производная функции f(x) по x . Теперь сформулируем правило нахождения производной обратной функции. Пусть функции y = f(x) и x = g(y) взаимно обратные, определенные на интервалах и соответственно. Если в точке существует конечная отличная от нуля производная функции f(x) , то в точке существует конечная производная обратной функции g(y) , причем . В другой записи . Можно это правило переформулировать для любого x из промежутка , тогда получим . Давайте проверим справедливость этих формул. Найдем обратную функцию для натурального логарифма (здесь y – функция, а x - аргумент). Разрешив это уравнение относительно x , получим (здесь x – функция, а y – ее аргумент). То есть, и взаимно обратные функции. Из таблицы производных видим, что и . Убедимся, что формулы нахождения производных обратной функции приводят нас к этим же результатам: